Concepts and Definitions
What is a ratio?
Ratios offer us a concise way to compare the size of one variable with another. For example, the ratio of job vacancies to unemployed persons compares the number of job openings with job seekers.
Ways to express a ratio
There are two common ways in which a ratio can be expressed.
Suppose we would like to compare variables A and B, with values equal to 5 for A and 4 for B. We can express the ratio of A to B in one of the two forms shown below.
Different Forms of Ratios and How to Interpret Them

Although in some instances the first ratio expression is more straight-forward, expressing a ratio as a decimal helps us compare two or more ratios. This is especially useful when comparing ratios across time or groups. For example, it is easier to see that 1.25 is greater than 1.20, than to compare 5:4 and 6:5.
Example 1 – Using ratios
Suppose we are comparing the wages for two occupations, A and B.
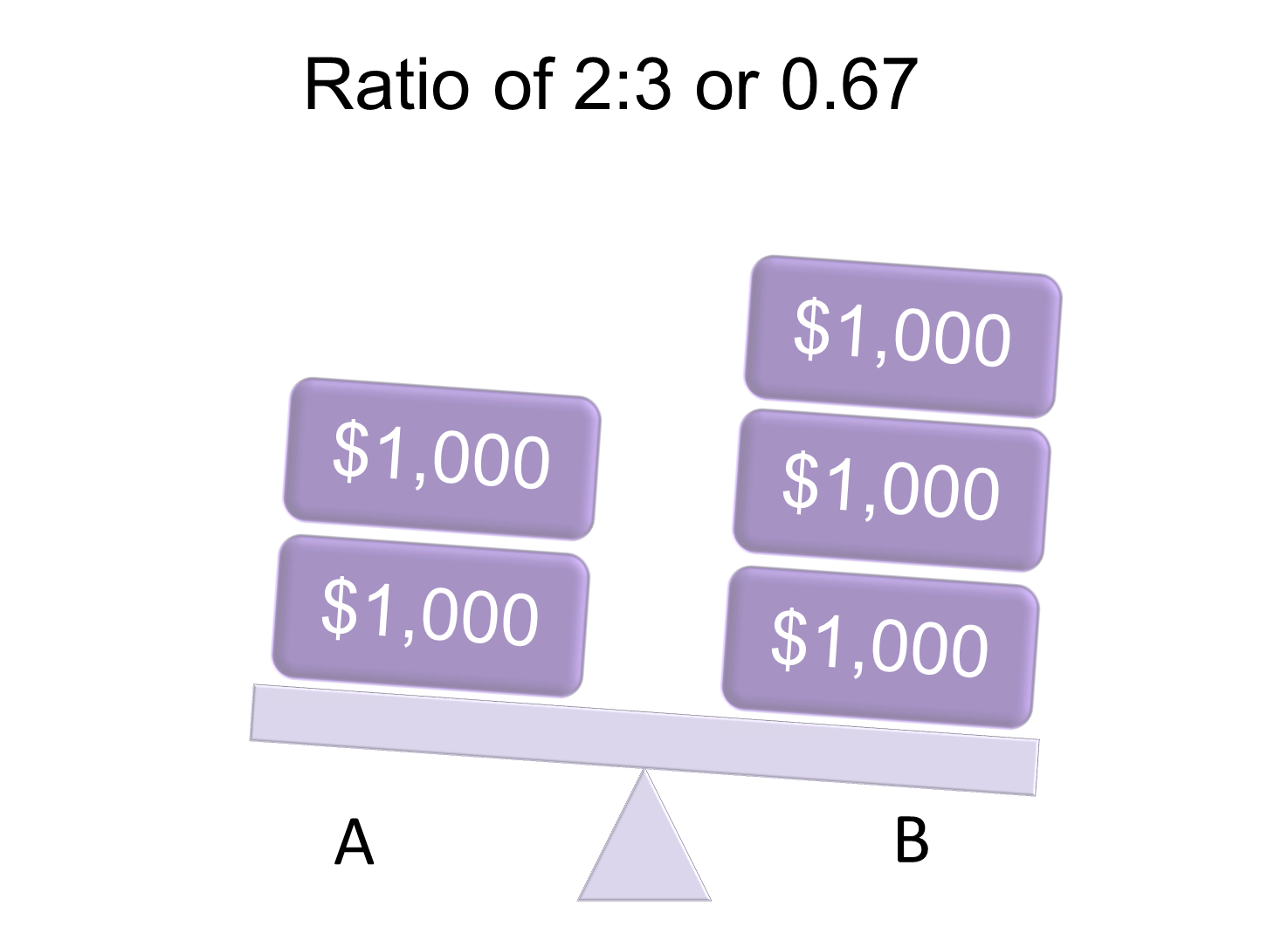
If the median monthly wage for occupation A is $2,000 and that for occupation B is $3,000, the ratio in decimal form is $2,000/$3,000 = 0.67. As the ratio is less than 1, the median wage for occupation A is less than the median wage for occupation B.
Occupation A Has Lower Median Wage Than Occupation B
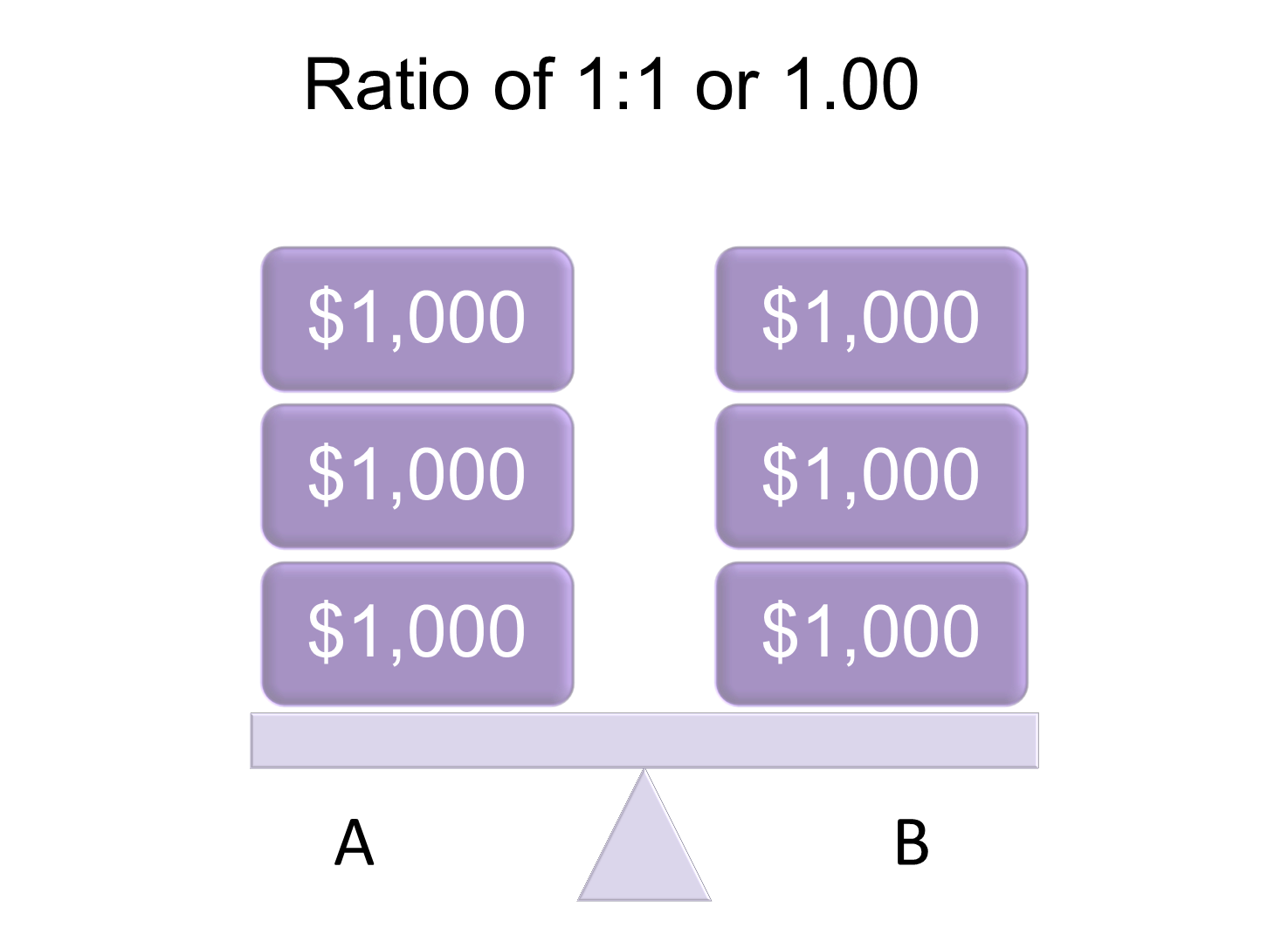
Now, what if the median wage for occupations A and B are both $3,000? The ratio of the wages in decimal form is 1.00, implying that the quantities compared have the same value.
Occupation A Has the Same Median Wage as Occupation B
Finally, suppose the median wage for occupation A is $3,000 and that for occupation B is $2,000. The ratio of the wages in decimal form is 1.50, which exceeds 1. This means that the first quantity (i.e. median wage of occupation A) is larger than the second quantity (median wage of occupation B).
Occupation A Has Higher Median Wage Than Occupation B